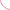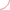Олимпиада по математике 2010-2011г.  (7 класс)

1. Таня пошла покупать ручки и карандаши. Целиком потратив деньги, она могла купить 6 ручек или 12 карандашей. Она решила на все деньги купить и поровну ручек и карандашей. Сколько ручек она купит?

2.  Близняшки Аня, Маня и Таня испекли на день рождения пирожные. Если бы Аня и Маня испекли в два раза больше пирожных, то общее число пирожных увеличилось бы на 60%. Какую долю пирожных в процентах испекла Таня?

3. На доске были записаны четыре натуральных числа. Сложив их всевозможными различными способами по два, Петя получил следующие шесть сумм: 17, 18, 20, 21, 23, 26. Докажите, что Петя ошибся при вычислении сумм.

4. У Пети имеется прямоугольник 5×7 и квадратик 1×1. Может ли Петя разрезать этот прямоугольник на 2 части, не являющиеся прямоугольниками, а потом из этих двух частей и данного квадратика 1×1 сложить квадрат 6×6? (Если это возможно, то должно быть показано, как разрезан прямоугольник и как составлен квадрат. Либо должно быть объяснено, почему это невозможно.)

5. Шесть друзей: Андрей, Витя, Боря, Саша, Толя и Гена, - выстроились в ряд в порядке убывания их роста (среди них нет имеющих одинаковый рост). Затем Гена и Андрей поменялись местами, Боря и Витя также поменялись местами и, наконец, Саша и Толя тоже поменялись местами. Оказалось, что теперь мальчики стоят в порядке возрастания их роста. Найдите самого высокого среди мальчиков, если известно, что Боря выше Андрея и Гены, но ниже Саши.

      6. На полоске 1´20 на 10 левых полях стоят 10 шашек. Шашка может ходить на соседнюю справа свободную клетку или перепрыгнуть через соседнюю справа шашку на следующую за ней клетку, если эта клетка свободна. Движение влево не разрешается. Можно ли все шашки переставить подряд без пробелов в обратном порядке?

Ответы: скачать Решение задач_7 класс_.doc

Олимпиада по математике 2010-2011г.  (8 класс)

1. В числе 333332222211111, записанном на доске, Петя стер три цифры и получил число, кратное 9. Какое число записано теперь на доске? (Указать все возможности и доказать, что других нет.)

2. Наташа и Инна купили по одинаковой коробке чая в пакетиках. Известно, что  с помощью одного пакетика они заваривали  две или три чашки чая. Этой коробки Наташе хватило на 53 чашки чая, а Инне — на 76. Сколько пакетиков было в коробке? Ответ должен быть обоснован.

3. Семь гномов различного возраста сидят за круглым столом. Известно, что каждый гном может говорить правду или ложь. Каждый из них сказал, что он старше своих соседей. Какое наибольшее количество правдивых утверждений могло быть?

4. Известно, что (x+y)/(x-y)+(x-y)/(x+y)=8. Найти (x^4+y^4)/(x^4-y^4)+(x^4-y^4)/(x^4+y^4).

5. Маленькие детки кушали конфетки. Каждый съел на 11 конфет меньше, чем все остальные вместе, но все же больше одной конфеты. Сколько всего конфет было съедено?

6.  На сторонах AB и AC треугольника ABC взяли точки K и D соответственно. Точку  E выбрали так, что K – середина отрезка DE. Оказалось, что угол EAK= угол ACB и AE=DC. Доказать, что BD – биссектриса угла ABC.

Ответы: скачать Решение задач_8 класс_.doc

Олимпиада по математике 2010-2011г.  (9 класс)

1. Куб натурального числа N делится на 2010. Следует ли отсюда, что само число N делится на 2010?

2. Имеются разные по размеру банки: А, Б, В и Г. Известно, что в 11 банок А и 7 банок Б вмещается столько же, сколько в 12 банок В. В 6 банок А и 5 банок Б вмещается столько же, сколько в 6 банок В и 1 банку Г. 6 банок Г полностью наполнены водой. Хватит ли 3 банки А и 8 банок Б, чтобы перелить всю воду из 6 банок Г?

3. Дан параллелограмм KLMN с острым углом при вершине K. На лучах KL и ML отмечены точки A и B соответственно, причём AM = LM и BK = KL.

а) Докажите, что AN = BN.

б) Докажите, что треугольники ABN и BKL подобны.

4. Доказать, что если уравнения x^2+ax+b=0 и -x^2+cx+d=0 оба не имеют корней, то уравнение 2010x^2+(1007a-1003c)x+1007b-1003d=0 не имеет корней.

5. Вася забыл четырехзначный код в камере хранения (код может быть любым от 0000 до 9999). Он помнит только, что число, задающее код, делится на 3 и на 7  и не делится на 5 и на 9. Сколько вариантов ему придется перебрать, чтобы наверняка угадать код?

6. Точки A и B взяты на графике функции y=2010/x, x>0. Из них опущены перпендикуляры на ось абсцисс, основания перпендикуляров - H_A и H_B; С – начало координат. Докажите, что площадь фигуры, ограниченной прямыми СA, СB и дугой AB, равна площади фигуры, ограниченной прямыми AH_A, BH_B, осью абсцисс и дугой AB.

Ответы: скачать Решение задач_9 класс_.doc

Олимпиада по математике 2010-2011г. (10 класс)

1. Докажите, что для всех натуральных n справедливо неравенство (n^n)(2010^2010)>=(n^2010)(2010^n) 

2. Может ли для какого-нибудь натурального k сумма цифр совпадать у следующих двух чисел (k+2009)(k+2010) и (k+2011)^2?

3. Квадратные трехчлены x^2+ax+b и x^2+cx+d имеют положительные вещественные корни x₁, x₂  и x₃, x₄ соответственно, причем x₁<x₃<x₂<x₄. Доказать, что квадратный трехчлен (a^2)(x^2)+2cdx+b^2 имеет корни.

4. Между каждыми двумя цифрами числа 1331 вставлено 2010 нулей. Докажите, что полученное число делится на 1331.

5. Окружность с центром на стороне BC равнобедренного треугольника ABC (AB=AC) касается сторон AB и AC. На сторонах AB и AC выбраны точки F и E соответственно, такие, что BF=3 и СE=2. Доказать, что отрезок FE касается данной окружности, если известно, что BC=2 корень из 6.

6. На плоскости расположены 2011 41-угольник. Известно, что любые два из них имеют ровно одну общую вершину. Доказать, что все 41-угольники имеют общую вершину.

Ответы: скачать Решение задач_10 класс_.doc

Олимпиада по математике 2010-2011г. (11 класс)

1. Докажите, что для всех натуральных  справедливо неравенство (n^n)(2010^2010)>=(n^2010)(2010^n)

2. Решить уравнение: x^8-x^6+x^4-x^2+1=0.

3. Существует ли функция заданная на множестве действительных чисел такая, что f(x^2)=x-2010 для всех действительных x?

4. Два пешехода обходят квадратный участок площадью 49 км² по его границе, выйдя одновременно из одного его угла в разные стороны и двигаясь с постоянными скоростями. Встретились они через 4 часа. Найдите скорости пешеходов, если известно, что через 2 часа пути расстоянии между ними было корень из 74 км.

5. В треугольник  ABC помещены три равных окружности, каждая из которых касается двух сторон треугольника. Все три окружности имеют одну общую точку и попарные пересечения. Найдите радиусы этих окружностей, если радиусы описанной и вписанной окружностей треугольника ABC равны R и r.

6. Уравнение x^4+ax^3+bx^2+c=0 имеет четыре различных действительных корня. Докажите, что bc<0.

Ответы: скачать Решение задач_11 класс_.doc